research!rsc

Thoughts and links about programming, by

RSS

Programming Language Memory Models
(Memory Models, Part 2)
Posted on Tuesday, July 6, 2021. PDF

Programming language memory models answer the question of what behaviors parallel programs can rely on to share memory between their threads. For example, consider this program in a C-like language, where both x and done start out zeroed. 

// Thread 1           // Thread 2
x = 1;                while(done == 0) { /* loop */ }
done = 1;             print(x);

The program attempts to send a message in x from thread 1 to thread 2, using done as the signal that the message is ready to be received. If thread 1 and thread 2, each running on its own dedicated processor, both run to completion, is this program guaranteed to finish and print 1, as intended? The programming language memory model answers that question and others like it.

Although each programming language differs in the details, a few general answers are true of essentially all modern multithreaded languages, including C, C++, Go, Java, JavaScript, Rust, and Swift:

Given how broken this program is, the obvious question is how to fix it.

Modern languages provide special functionality, in the form of atomic variables or atomic operations, to allow a program to synchronize its threads. If we make done an atomic variable (or manipulate it using atomic operations, in languages that take that approach), then our program is guaranteed to finish and to print 1. Making done atomic has many effects:

The end result of making done atomic is that the program behaves as we want, successfully passing the value in x from thread 1 to thread 2.

In the original program, after the compiler’s code reordering, thread 1 could be writing x at the same moment that thread 2 was reading it. This is a data race. In the revised program, the atomic variable done serves to synchronize access to x: it is now impossible for thread 1 to be writing x at the same moment that thread 2 is reading it. The program is data-race-free. In general, modern languages guarantee that data-race-free programs always execute in a sequentially consistent way, as if the operations from the different threads were interleaved, arbitrarily but without reordering, onto a single processor. This is the DRF-SC property from hardware memory models, adopted in the programming language context.

As an aside, these atomic variables or atomic operations would more properly be called “synchronizing atomics.” It’s true that the operations are atomic in the database sense, allowing simultaneous reads and writes which behave as if run sequentially in some order: what would be a race on ordinary variables is not a race when using atomics. But it’s even more important that the atomics synchronize the rest of the program, providing a way to eliminate races on the non-atomic data. The standard terminology is plain “atomic”, though, so that’s what this post uses. Just remember to read “atomic” as “synchronizing atomic” unless noted otherwise.

The programming language memory model specifies the exact details of what is required from programmers and from compilers, serving as a contract between them. The general features sketched above are true of essentially all modern languages, but it is only recently that things have converged to this point: in the early 2000s, there was significantly more variation. Even today there is significant variation among languages on second-order questions, including:

After some preliminaries, the rest of this post examines how different languages answer these and related questions, along with the paths they took to get there. The post also highlights the many false starts along the way, to emphasize that we are still very much learning what works and what does not.

Hardware, Litmus Tests, Happens Before, and DRF-SC

Before we get to details of any particular language, a brief summary of lessons from hardware memory models that we will need to keep in mind.

Different architectures allow different amounts of reordering of instructions, so that code running in parallel on multiple processors can have different allowed results depending on the architecture. The gold standard is sequential consistency, in which any execution must behave as if the programs executed on the different processors were simply interleaved in some order onto a single processor. That model is much easier for developers to reason about, but no significant architecture provides it today, because of the performance gains enabled by weaker guarantees.

It is difficult to make completely general statements comparing different memory models. Instead, it can help to focus on specific test cases, called litmus tests. If two memory models allow different behaviors for a given litmus test, this proves they are different and usually helps us see whether, at least for that test case, one is weaker or stronger than the other. For example, here is the litmus test form of the program we examined earlier:

Litmus Test: Message Passing
Can this program see r1 = 1, r2 = 0?

// Thread 1           // Thread 2
x = 1                 r1 = y
y = 1                 r2 = x

On sequentially consistent hardware: no.
On x86 (or other TSO): no.
On ARM/POWER: yes!
In any modern compiled language using ordinary variables: yes!

As in the previous post, we assume every example starts with all shared variables set to zero. The name rN denotes private storage like a register or function-local variable; the other names like x and y are distinct, shared (global) variables. We ask whether a particular setting of registers is possible at the end of an execution. When answering the litmus test for hardware, we assume that there’s no compiler to reorder what happens in the thread: the instructions in the listings are directly translated to assembly instructions given to the processor to execute.

The outcome r1 = 1, r2 = 0 corresponds to the original program’s thread 2 finishing its loop (done is y) but then printing 0. This result is not possible in any sequentially consistent interleaving of the program operations. For an assembly language version, printing 0 is not possible on x86, although it is possible on more relaxed architectures like ARM and POWER due to reordering optimizations in the processors themselves. In a modern language, the reordering that can happen during compilation makes this outcome possible no matter what the underlying hardware.

Instead of guaranteeing sequential consistency, as we mentioned earlier, today’s processors guarantee a property called “data-race-free sequential-consistency”, or DRF-SC (sometimes also written SC-DRF). A system guaranteeing DRF-SC must define specific instructions called synchronizing instructions, which provide a way to coordinate different processors (equivalently, threads). Programs use those instructions to create a “happens before” relationship between code running on one processor and code running on another.

For example, here is a depiction of a short execution of a program on two threads; as usual, each is assumed to be on its own dedicated processor:

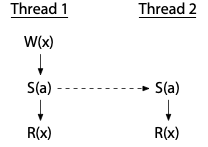
We saw this program in the previous post too. Thread 1 and thread 2 execute a synchronizing instruction S(a). In this particular execution of the program, the two S(a) instructions establish a happens-before relationship from thread 1 to thread 2, so the W(x) in thread 1 happens before the R(x) in thread 2.

Two events on different processors that are not ordered by happens-before might occur at the same moment: the exact order is unclear. We say they execute concurrently. A data race is when a write to a variable executes concurrently with a read or another write of that same variable. Processors that provide DRF-SC (all of them, these days) guarantee that programs without data races behave as if they were running on a sequentially consistent architecture. This is the fundamental guarantee that makes it possible to write correct multithreaded assembly programs on modern processors.

As we saw earlier, DRF-SC is also the fundamental guarantee that modern languages have adopted to make it possible to write correct multithreaded programs in higher-level languages.

Compilers and Optimizations

We have mentioned a couple times that compilers might reorder the operations in the input program in the course of generating the final executable code. Let’s take a closer look at that claim and at other optimizations that might cause problems.

It is generally accepted that a compiler can reorder ordinary reads from and writes to memory almost arbitrarily, provided the reordering cannot change the observed single-threaded execution of the code. For example, consider this program: 

w = 1
x = 2
r1 = y
r2 = z

Since w, x, y, and z are all different variables, these four statements can be executed in any order deemed best by the compiler.

As we noted above, the ability to reorder reads and writes so freely makes the guarantees of ordinary compiled programs at least as weak as the ARM/POWER relaxed memory model, since compiled programs fail the message passing litmus test. In fact, the guarantees for compiled programs are weaker.

In the hardware post, we looked at coherence as an example of something that ARM/POWER architectures do guarantee:

Litmus Test: Coherence
Can this program see r1 = 1, r2 = 2, r3 = 2, r4 = 1?
(Can Thread 3 see x = 1 before x = 2 while Thread 4 sees the reverse?)

// Thread 1    // Thread 2    // Thread 3    // Thread 4
x = 1          x = 2          r1 = x         r3 = x
                              r2 = x         r4 = x

On sequentially consistent hardware: no.
On x86 (or other TSO): no.
On ARM/POWER: no.
In any modern compiled language using ordinary variables: yes!

All modern hardware guarantees coherence, which can also be viewed as sequential consistency for the operations on a single memory location. In this program, one of the writes must overwrite the other, and the entire system has to agree about which is which. It turns out that, because of program reordering during compilation, modern languages do not even provide coherence.

Suppose the compiler reorders the two reads in thread 4, and then the instructions run as if interleaved in this order: 

// Thread 1    // Thread 2    // Thread 3    // Thread 4
                                             // (reordered)
(1) x = 1                     (2) r1 = x     (3) r4 = x
               (4) x = 2      (5) r2 = x     (6) r3 = x

The result is r1 = 1, r2 = 2, r3 = 2, r4 = 1, which was impossible in the assembly programs but possible in high-level languages. In this sense, programming language memory models are all weaker than the most relaxed hardware memory models.

But there are some guarantees. Everyone agrees on the need to provide DRF-SC, which disallows optimizations that introduce new reads or writes, even if those optimizations would have been valid in single-threaded code.

For example, consider this code: 

if(c) {
    x++;
} else {
    ... lots of code ...
}

There’s an if statement with lots of code in the else and only an x++ in the if body. It might be cheaper to have fewer branches and eliminate the if body entirely. We can do that by running the x++ before the if and then adjusting with an x-- in the big else body if we were wrong. That is, the compiler might consider rewriting that code to: 

x++;
if(!c) {
    x--;
    ... lots of code ...
}

Is this a safe compiler optimization? In a single-threaded program, yes. In a multithreaded program in which x is shared with another thread when c is false, no: the optimization would introduce a race on x that was not present in the original program.

This example is derived from one in Hans Boehm’s 2004 paper, “Threads Cannot Be Implemented As a Library,” which makes the case that languages cannot be silent about the semantics of multithreaded execution.

The programming language memory model is an attempt to precisely answer these questions about which optimizations are allowed and which are not. By examining the history of attempts at writing these models over the past couple decades, we can learn what worked and what didn’t, and get a sense of where things are headed.

Original Java Memory Model (1996)

Java was the first mainstream language to try to write down what it guaranteed to multithreaded programs. It included mutexes and defined the memory ordering requirements they implied. It also included “volatile” atomic variables: all the reads and writes of volatile variables were required to execute in program order directly in main memory, making the operations on volatile variables behave in a sequentially consistent manner. Finally, Java also specified (or at least attempted to specify) the behavior of programs with data races. One part of this was to mandate a form of coherence for ordinary variables, which we will examine more below. Unfortunately, this attempt, in the first edition of the Java Language Specification (1996), had at least two serious flaws. They are easy to explain with the benefit of hindsight and using the preliminaries we’ve already set down. At the time, they were far less obvious.

Atomics need to synchronize

The first flaw was that volatile atomic variables were non-synchronizing, so they did not help eliminate races in the rest of the program. The Java version of the message passing program we saw above would be: 

int x;
volatile int done;

// Thread 1           // Thread 2
x = 1;                while(done == 0) { /* loop */ }
done = 1;             print(x);

Because done is declared volatile, the loop is guaranteed to finish: the compiler cannot cache it in a register and cause an infinite loop. However, the program is not guaranteed to print 1. The compiler was not prohibited from reordering the accesses to x and done, nor was it required to prohibit the hardware from doing the same.

Because Java volatiles were non-synchronizing atomics, you could not use them to build new synchronization primitives. In this sense, the original Java memory model was too weak.

Coherence is incompatible with compiler optimizations

The orginal Java memory model was also too strong: mandating coherence—once a thread had read a new value of a memory location, it could not appear to later read the old value—disallowed basic compiler optimizations. Earlier we looked at how reordering reads would break coherence, but you might think, well, just don’t reorder reads. Here’s a more subtle way coherence might be broken by another optimization: common subexpression elimination.

Consider this Java program: 

// p and q may or may not point at the same object.
int i = p.x;
// ... maybe another thread writes p.x at this point ...
int j = q.x;
int k = p.x;

In this program, common subexpression elimination would notice that p.x is computed twice and optimize the final line to k = i. But if p and q pointed to the same object and another thread wrote to p.x between the reads into i and j, then reusing the old value i for k violates coherence: the read into i saw an old value, the read into j saw a newer value, but then the read into k reusing i would once again see the old value. Not being able to optimize away redundant reads would hobble most compilers, making the generated code slower.

Coherence is easier for hardware to provide than for compilers because hardware can apply dynamic optimizations: it can adjust the optimization paths based on the exact addresses involved in a given sequence of memory reads and writes. In contrast, compilers can only apply static optimizations: they have to write out, ahead of time, an instruction sequence that will be correct no matter what addresses and values are involved. In the example, the compiler cannot easily change what happens based on whether p and q happen to point to the same object, at least not without writing out code for both possibilities, leading to significant time and space overheads. The compiler’s incomplete knowledge about the possible aliasing between memory locations means that actually providing coherence would require giving up fundamental optimizations.

Bill Pugh identified this and other problems in his 1999 paper “Fixing the Java Memory Model.”

New Java Memory Model (2004)

Because of these problems, and because the original Java Memory Model was difficult even for experts to understand, Pugh and others started an effort to define a new memory model for Java. That model became JSR-133 and was adopted in Java 5.0, released in 2004. The canonical reference is “The Java Memory Model” (2005), by Jeremy Manson, Bill Pugh, and Sarita Adve, with additional details in Manson’s Ph.D. thesis. The new model follows the DRF-SC approach: Java programs that are data-race-free are guaranteed to execute in a sequentially consistent manner.

Synchronizing atomics and other operations

As we saw earlier, to write a data-race-free program, programmers need synchronization operations that can establish happens-before edges to ensure that one thread does not write a non-atomic variable concurrently with another thread reading or writing it. In Java, the main synchronization operations are:

What does “subsequent” mean? Java defines that all lock, unlock, and volatile variable accesses behave as if they ocurred in some sequentially consistent interleaving, giving a total order over all those operations in the entire program. “Subsequent” means later in that total order. That is: the total order over lock, unlock, and volatile variable accesses defines the meaning of subsequent, then subsequent defines which happens-before edges are created by a particular execution, and then the happens-before edges define whether that particular execution had a data race. If there is no race, then the execution behaves in a sequentially consistent manner.

The fact that the volatile accesses must act as if in some total ordering means that in the store buffer litmus test, you can’t end up with r1 = 0 and r2 = 0:

Litmus Test: Store Buffering
Can this program see r1 = 0, r2 = 0?

// Thread 1           // Thread 2
x = 1                 y = 1
r1 = y                r2 = x

On sequentially consistent hardware: no.
On x86 (or other TSO): yes!
On ARM/POWER: yes!
On Java using volatiles: no.

In Java, for volatile variables x and y, the reads and writes cannot be reordered: one write has to come second, and the read that follows the second write must see the first write. If we didn’t have the sequentially consistent requirement—if, say, volatiles were only required to be coherent—the two reads could miss the writes.

There is an important but subtle point here: the total order over all the synchronizing operations is separate from the happens-before relationship. It is not true that there is a happens-before edge in one direction or the other between every lock, unlock, or volatile variable access in a program: you only get a happens-before edge from a write to a read that observes the write. For example, a lock and unlock of different mutexes have no happens-before edges between them, nor do volatile accesses of different variables, even though collectively these operations must behave as if following a single sequentially consistent interleaving.

Semantics for racy programs

DRF-SC only guarantees sequentially consistent behavior to programs with no data races. The new Java memory model, like the original, defined the behavior of racy programs, for a number of reasons:

Instead of relying on coherence, the new model reused the happens-before relation (already used to decide whether a program had a race at all) to decide the outcome of racing reads and writes.

The specific rules for Java are that for word-sized or smaller variables, a read of a variable (or field) x must see the value stored by some single write to x. A write to x can be observed by a read r provided r does not happen before w. That means r can observe writes that happen before r (but that aren’t also overwritten before r), and it can observe writes that race with r.

Using happens-before in this way, combined with synchronizing atomics (volatiles) that could establish new happens-before edges, was a major improvement over the original Java memory model. It provided more useful guarantees to the programmer, and it made a large number of important compiler optimizations definitively allowed. This work is still the memory model for Java today. That said, it’s also still not quite right: there are problems with this use of happens-before for trying to define the semantics of racy programs.

Happens-before does not rule out incoherence

The first problem with happens-before for defining program semantics has to do with coherence (again!). (The following example is taken from Jaroslav Ševčík and David Aspinall’s paper, “On the Validity of Program Transformations in the Java Memory Model” (2007).)

Here’s a program with three threads. Let’s assume that Thread 1 and Thread 2 are known to finish before Thread 3 starts. 

// Thread 1           // Thread 2           // Thread 3
lock(m1)              lock(m2)
x = 1                 x = 2
unlock(m1)            unlock(m2)
                                            lock(m1)
                                            lock(m2)
                                            r1 = x
                                            r2 = x
                                            unlock(m2)
                                            unlock(m1)

Thread 1 writes x = 1 while holding mutex m1. Thread 2 writes x = 2 while holding mutex m2. Those are different mutexes, so the two writes race. However, only thread 3 reads x, and it does so after acquiring both mutexes. The read into r1 can read either write: both happen before it, and neither definitively overwrites the other. By the same argument, the read into r2 can read either write. But strictly speaking, nothing in the Java memory model says the two reads have to agree: technically, r1 and r2 can be left having read different values of x. That is, this program can end with r1 and r2 holding different values. Of course, no real implementation is going to produce different r1 and r2. Mutual exclusion means there are no writes happening between those two reads. They have to get the same value. But the fact that the memory model allows different reads shows that it is, in a certain technical way, not precisely describing real Java implementations.

The situation gets worse. What if we add one more instruction, x = r1, between the two reads: 

// Thread 1           // Thread 2           // Thread 3
lock(m1)              lock(m2)
x = 1                 x = 2
unlock(m1)            unlock(m2)
                                            lock(m1)
                                            lock(m2)
                                            r1 = x
                                            x = r1   // !?
                                            r2 = x
                                            unlock(m2)
                                            unlock(m1)

Now, clearly the r2 = x read must use the value written by x = r1, so the program must get the same values in r1 and r2. The two values r1 and r2 are now guaranteed to be equal.

The difference between these two programs means we have a problem for compilers. A compiler that sees r1 = x followed by x = r1 may well want to delete the second assignment, which is “clearly” redundant. But that “optimization” changes the second program, which must see the same values in r1 and r2, into the first program, which technically can have r1 different from r2. Therefore, according to the Java Memory Model, this optimization is technically invalid: it changes the meaning of the program. To be clear, this optimization would not change the meaning of Java programs executing on any real JVM you can imagine. But somehow the Java Memory Model doesn’t allow it, suggesting there’s more that needs to be said.

For more about this example and others, see Ševčík and Aspinall’s paper.

Happens-before does not rule out acausality

That last example turns out to have been the easy problem. Here’s a harder problem. Consider this litmus test, using ordinary (not volatile) Java variables:

Litmus Test: Racy Out Of Thin Air Values
Can this program see r1 = 42, r2 = 42?

// Thread 1           // Thread 2
r1 = x                r2 = y
y = r1                x = r2

(Obviously not!)

All the variables in this program start out zeroed, as always, and then this program effectively runs y = x in one thread and x = y in the other thread. Can x and y end up being 42? In real life, obviously not. But why not? The memory model turns out not to disallow this result.

Suppose hypothetically that “r1 = x” did read 42. Then “y = r1” would write 42 to y, and then the racing “r2 = y” could read 42, causing the “x = r2” to write 42 to x, and that write races with (and is therefore observable by) the original “r1 = x,” appearing to justify the original hypothetical. In this example, 42 is called an out-of-thin-air value, because it appeared without any justification but then justified itself with circular logic. What if the memory had formerly held a 42 before its current 0, and the hardware incorrectly speculated that it was still 42? That speculation might become a self-fulfilling prophecy. (This argument seemed more far-fetched before Spectre and related attacks showed just how aggressively hardware speculates. Even so, no hardware invents out-of-thin-air values this way.)

It seems clear that this program cannot end with r1 and r2 set to 42, but happens-before doesn’t by itself explain why this can’t happen. That suggests again that there’s a certain incompleteness. The new Java Memory Model spends a lot of time addressing this incompleteness, about which more shortly.

This program has a race—the reads of x and y are racing against writes in the other threads—so we might fall back on arguing that it’s an incorrect program. But here is a version that is data-race-free:

Litmus Test: Non-Racy Out Of Thin Air Values
Can this program see r1 = 42, r2 = 42?

// Thread 1           // Thread 2
r1 = x                r2 = y
if (r1 == 42)         if (r2 == 42)
    y = r1                x = r2

(Obviously not!)

Since x and y start out zero, any sequentially consistent execution is never going to execute the writes, so this program has no writes, so there are no races. Once again, though, happens-before alone does not exclude the possibility that, hypothetically, r1 = x sees the racing not-quite-write, and then following from that hypothetical, the conditions both end up true and x and y are both 42 at the end. This is another kind of out-of-thin-air value, but this time in a program with no race. Any model guaranteeing DRF-SC must guarantee that this program only sees all zeros at the end, yet happens-before doesn’t explain why.

The Java memory model spends a lot of words that I won’t go into to try to exclude these kinds of acausal hypotheticals. Unfortunately, five years later, Sarita Adve and Hans Boehm had this to say about that work:

Prohibiting such causality violations in a way that does not also prohibit other desired optimizations turned out to be surprisingly difficult. … After many proposals and five years of spirited debate, the current model was approved as the best compromise. … Unfortunately, this model is very complex, was known to have some surprising behaviors, and has recently been shown to have a bug.

(Adve and Boehm, “Memory Models: A Case For Rethinking Parallel Languages and Hardware,” August 2010)

C++11 Memory Model (2011)

Let’s put Java to the side and examine C++. Inspired by the apparent success of Java’s new memory model, many of the same people set out to define a similar memory model for C++, eventually adopted in C++11. Compared to Java, C++ deviated in two important ways. First, C++ makes no guarantees at all for programs with data races, which would seem to remove the need for much of the complexity of the Java model. Second, C++ provides three kinds of atomics: strong synchronization (“sequentially consistent”), weak synchronization (“acquire/release”, coherence-only), and no synchronization (“relaxed”, for hiding races). The relaxed atomics reintroduced all of Java’s complexity about defining the meaning of what amount to racy programs. The result is that the C++ model is more complicated than Java’s yet less helpful to programmers.

C++11 also defined atomic fences as an alternative to atomic variables, but they are not as commonly used and I’m not going to discuss them.

DRF-SC or Catch Fire

Unlike Java, C++ gives no guarantees to programs with races. Any program with a race anywhere in it falls into “undefined behavior.” A racing access in the first microseconds of program execution is allowed to cause arbitrary errant behavior hours or days later. This is often called “DRF-SC or Catch Fire”: if the program is data-race free it runs in a sequentially consistent manner, and if not, it can do anything at all, including catch fire.

For a longer presentation of the arguments for DRF-SC or Catch Fire, see Boehm, “Memory Model Rationales” (2007) and Boehm and Adve, “Foundations of the C++ Concurrency Memory Model” (2008).

Briefly, there are four common justifications for this position:

Personally, the last justification is the only one I find compelling, although I observe that it is possible to say “race detectors are allowed” without also saying “one race on an integer can invalidate your entire program.”

Here is an example from “Memory Model Rationales” that I think captures the essence of the C++ approach as well as its problems. Consider this program, which refers to a global variable x. 

unsigned i = x;

if (i < 2) {
    foo: ...
    switch (i) {
    case 0:
        ...;
        break;
    case 1:
        ...;
        break;
    }
}

The claim is that a C++ compiler might be holding i in a register but then need to reuse the registers if the code at label foo is complex. Rather than spill the current value of i to the function stack, the compiler might instead decide to load i a second time from the global x upon reaching the switch statement. The result is that, halfway through the if body, i < 2 may stop being true. If the compiler did something like compiling the switch into a computed jump using a table indexed by i, that code would index off the end of the table and jump to an unexpected address, which could be arbitrarily bad.

From this example and others like it, the C++ memory model authors conclude that any racy access must be allowed to cause unbounded damage to the future execution of the program. Personally, I conclude instead that in a multithreaded program, compilers should not assume that they can reload a local variable like i by re-executing the memory read that initialized it. It may well have been impractical to expect existing C++ compilers, written for a single-threaded world, to find and fix code generation problems like this one, but in new languages, I think we should aim higher.

Digression: Undefined behavior in C and C++

As an aside, the C and C++ insistence on the compiler’s ability to behave arbitrarily badly in response to bugs in programs leads to truly ridiculous results. For example, consider this program, which was a topic of discussion on Twitter in 2017: 

#include <cstdlib>

typedef int (*Function)();

static Function Do;

static int EraseAll() {
    return system("rm -rf slash");
}

void NeverCalled() {
    Do = EraseAll;
}

int main() {
    return Do();
}

If you were a modern C++ compiler like Clang, you might think about this program as follows:

The end result is that Clang optimizes the program down to: 

int main() {
    return system("rm -rf slash");
}

You have to admit: next to this example, the possibility that the local variable i might suddenly stop being less than 2 halfway through the body of if (i < 2) does not seem out of place.

In essence, modern C and C++ compilers assume no programmer would dare attempt undefined behavior. A programmer writing a program with a bug? Inconceivable!

Like I said, in new languages I think we should aim higher.

Acquire/release atomics

C++ adopted sequentially consistent atomic variables much like (new) Java’s volatile variables (no relation to C++ volatile). In our message passing example, we can declare done as 

atomic<int> done;

and then use done as if it were an ordinary variable, like in Java. Or we can declare an ordinary int done; and then use 

atomic_store(&done, 1);

and 

while(atomic_load(&done) == 0) { /* loop */ }

to access it. Either way, the operations on done take part in the sequentially consistent total order on atomic operations and synchronize the rest of the program.

C++ also added weaker atomics, which can be accessed using atomic_store_explicit and atomic_load_explicit with an additional memory ordering argument. Using memory_order_seq_cst makes the explicit calls equivalent to the shorter ones above.

The weaker atomics are called acquire/release atomics, in which a release observed by a later acquire creates a happens-before edge from the release to the acquire. The terminology is meant to evoke mutexes: release is like unlocking a mutex, and acquire is like locking that same mutex. The writes executed before the release must be visible to reads executed after the subsequent acquire, just as writes executed before unlocking a mutex must be visible to reads executed after later locking that same mutex.

To use the weaker atomics, we could change our message-passing example to use 

atomic_store(&done, 1, memory_order_release);

and 

while(atomic_load(&done, memory_order_acquire) == 0) { /* loop */ }

and it would still be correct. But not all programs would.

Recall that the sequentially consistent atomics required the behavior of all the atomics in the program to be consistent with some global interleaving—a total order—of the execution. Acquire/release atomics do not. They only require a sequentially consistent interleaving of the operations on a single memory location. That is, they only require coherence. The result is that a program using acquire/release atomics with more than one memory location may observe executions that cannot be explained by a sequentially consistent interleaving of all the acquire/release atomics in the program, arguably a violation of DRF-SC!

To show the difference, here’s the store buffer example again:

Litmus Test: Store Buffering
Can this program see r1 = 0, r2 = 0?

// Thread 1           // Thread 2
x = 1                 y = 1
r1 = y                r2 = x

On sequentially consistent hardware: no.
On x86 (or other TSO): yes!
On ARM/POWER: yes!
On Java (using volatiles): no.
On C++11 (sequentially consistent atomics): no.
On C++11 (acquire/release atomics): yes!

The C++ sequentially consistent atomics match Java’s volatile. But the acquire-release atomics impose no relationship between the orderings for x and the orderings for y. In particular, it is allowed for the program to behave as if r1 = y happened before y = 1 while at the same time r2 = x happened before x = 1, allowing r1 = 0, r2 = 0 in contradiction of whole-program sequential consistency. These probably exist only because they are free on x86.

Note that, for a given set of specific reads observing specific writes, C++ sequentially consistent atomics and C++ acquire/release atomics create the same happens-before edges. The difference between them is that some sets of specific reads observing specific writes are disallowed by sequentially consistent atomics but allowed by acquire/release atomics. One such example is the set that leads to r1 = 0, r2 = 0 in the store buffering case.

A real example of the weakness of acquire/release

Acquire/release atomics are less useful in practice than atomics providing sequential consistency. Here is an example. Suppose we have a new synchronization primitive, a single-use condition variable with two methods Notify and Wait. For simplicity, only a single thread will call Notify and only a single thread will call Wait. We want to arrange for Notify to be lock-free when the other thread is not yet waiting. We can do this with a pair of atomic integers: 

class Cond {
    atomic<int> done;
    atomic<int> waiting;
    ...
};

void Cond::notify() {
    done = 1;
    if (!waiting)
        return;
    // ... wake up waiter ...
}

void Cond::wait() {
    waiting = 1;
    if(done)
        return;
    // ... sleep ...
}

The important part about this code is that notify sets done before checking waiting, while wait sets waiting before checking done, so that concurrent calls to notify and wait cannot result in notify returning immediately and wait sleeping. But with C++ acquire/release atomics, they can. And they probably would only some fraction of time, making the bug very hard to reproduce and diagnose. (Worse, on some architectures like 64-bit ARM, the best way to implement acquire/release atomics is as sequentially consistent atomics, so you might write code that works fine on 64-bit ARM and only discover it is incorrect when porting to other systems.)

With this understanding, “acquire/release” is an unfortunate name for these atomics, since the sequentially consistent ones do just as much acquiring and releasing. What’s different about these is the loss of sequential consistency. It might have been better to call these “coherence” atomics. Too late.

Relaxed atomics

C++ did not stop with the merely coherent acquire/release atomics. It also introduced non-synchronizing atomics, called relaxed atomics (memory_order_relaxed). These atomics have no synchronizing effect at all—they create no happens-before edges—and they have no ordering guarantees at all either. In fact, there is no difference between a relaxed atomic read/write and an ordinary read/write except that a race on relaxed atomics is not considered a race and cannot catch fire.

Much of the complexity of the revised Java memory model arises from defining the behavior of programs with data races. It would be nice if C++‘s adoption of DRF-SC or Catch Fire—effectively disallowing programs with data races—meant that we could throw away all those strange examples we looked at earlier, so that the C++ language spec would end up simpler than Java’s. Unfortunately, including the relaxed atomics ends up preserving all those concerns, meaning the C++11 spec ended up no simpler than Java’s.

Like Java’s memory model, the C++11 memory model also ended up incorrect. Consider the data-race-free program from before:

Litmus Test: Non-Racy Out Of Thin Air Values
Can this program see r1 = 42, r2 = 42?

// Thread 1           // Thread 2
r1 = x                r2 = y
if (r1 == 42)         if (r2 == 42)
    y = r1                x = r2

(Obviously not!)

C++11 (ordinary variables): no.
C++11 (relaxed atomics): yes!

In their paper “Common Compiler Optimisations are Invalid in the C11 Memory Model and what we can do about it” (2015), Viktor Vafeiadis and others showed that the C++11 specification guarantees that this program must end with x and y set to zero when x and y are ordinary variables. But if x and y are relaxed atomics, then, strictly speaking, the C++11 specification does not rule out that r1 and r2 might both end up 42. (Surprise!)

See the paper for the details, but at a high level, the C++11 spec had some formal rules trying to disallow out-of-thin-air values, combined with some vague words to discourage other kinds of problematic values. Those formal rules were the problem, so C++14 dropped them and left only the vague words. Quoting the rationale for removing them, the C++11 formulation turned out to be “both insufficient, in that it leaves it largely impossible to reason about programs with memory_order_relaxed, and seriously harmful, in that it arguably disallows all reasonable implementations of memory_order_relaxed on architectures like ARM and POWER.”

To recap, Java tried to exclude all acausal executions formally and failed. Then, with the benefit of Java’s hindsight, C++11 tried to exclude only some acausal executions formally and also failed. C++14 then said nothing formal at all. This is not going in the right direction.

In fact, a paper by Mark Batty and others from 2015 titled “The Problem of Programming Language Concurrency Semantics” gave this sobering assessment:

Disturbingly, 40+ years after the first relaxed-memory hardware was introduced (the IBM 370/158MP), the field still does not have a credible proposal for the concurrency semantics of any general-purpose high-level language that includes high-performance shared-memory concurrency primitives.

Even defining the semantics of weakly-ordered hardware (ignoring the complications of software and compiler optimization) is not going terribly well. A paper by Sizhuo Zhang and others in 2018 titled “Constructing a Weak Memory Model” recounted more recent events:

Sarkar et al. published an operational model for POWER in 2011, and Mador-Haim et al. published an axiomatic model that was proven to match the operational model in 2012. However, in 2014, Alglave et al. showed that the original operational model, as well as the corresponding axiomatic model, ruled out a newly observed behavior on POWER machines. For another instance, in 2016, Flur et al. gave an operational model for ARM, with no corresponding axiomatic model. One year later, ARM released a revision in their ISA manual explicitly forbidding behaviors allowed by Flur’s model, and this resulted in another proposed ARM memory model. Clearly, formalizing weak memory models empirically is error-prone and challenging.

The researchers who have been working to define and formalize all of this over the past decade are incredibly smart, talented, and persistent, and I don’t mean to detract from their efforts and accomplishments by pointing out inadequacies in the results. I conclude from those simply that this problem of specifying the exact behavior of threaded programs, even without races, is incredibly subtle and difficult. Today, it seems still beyond the grasp of even the best and brightest researchers. Even if it weren’t, a programming language definition works best when it is understandable by everyday developers, without the requirement of spending a decade studying the semantics of concurrent programs.

C, Rust and Swift Memory Models

C11 adopted the C++11 memory model as well, making it the C/C++11 memory model.

Rust 1.0.0 in 2015 and Swift 5.3 in 2020 both adopted the C/C++ memory model in its entirety, with DRF-SC or Catch Fire and all the atomic types and atomic fences.

It is not surprising that both of these languages adopted the C/C++ model, since they are built on a C/C++ compiler toolchain (LLVM) and emphasize close integration with C/C++ code.

Hardware Digression: Efficient Sequentially Consistent Atomics

Early multiprocessor architectures had a variety of synchronization mechanisms and memory models, with varying degrees of usability. In this diversity, the efficiency of different synchronization abstractions depended on how well they mapped to what the architecture provided. To construct the abstraction of sequentially consistent atomic variables, sometimes the only choice was to use barriers that did more and were far more expensive than strictly necessary, especially on ARM and POWER.

With C, C++, and Java all providing this same abstraction of sequentially consistent synchronizing atomics, it behooves hardware designers to make that abstraction efficient. The ARMv8 architecture (both 32- and 64-bit) introduced ldar and stlr load and store instructions, providing a direct implementation. In a talk in 2017, Herb Sutter claimed that IBM had approved him saying that they intended future POWER implementations to have some kind of more efficient support for sequentially consistent atomics as well, giving programmers “less reason to use relaxed atomics.” I can’t tell whether that happened, although here in 2021, POWER has turned out to be much less relevant than ARMv8.

The effect of this convergence is that sequentially consistent atomics are now well understood and can be efficiently implemented on all major hardware platforms, making them a good target for programming language memory models.

JavaScript Memory Model (2017)

You might think that JavaScript, a notoriously single-threaded language, would not need to worry about a memory model for what happens when code runs in parallel on multiple processors. I certainly did. But you and I would be wrong.

JavaScript has web workers, which allow running code in another thread. As originally conceived, workers only communicated with the main JavaScript thread by explicit message copying. With no shared writable memory, there was no need to consider issues like data races. However, ECMAScript 2017 (ES2017) added the SharedArrayBuffer object, which lets the main thread and workers share a block of writable memory. Why do this? In an early draft of the proposal, the first reason listed is compiling multithreaded C++ code to JavaScript.

Of course, having shared writable memory also requires defining atomic operations for synchronization and a memory model. JavaScript deviates from C++ in three important ways:

Precisely defining the behavior of racy programs leads to the usual complexities of relaxed memory semantics and how to disallow out-of-thin-air reads and the like. In addition to those challenges, which are mostly the same as elsewhere, the ES2017 definition had two interesting bugs that arose from a mismatch with the semantics of the new ARMv8 atomic instructions. These examples are adapted from Conrad Watt et al.’s 2020 paper “Repairing and Mechanising the JavaScript Relaxed Memory Model.”

As we noted in the previous section, ARMv8 added ldar and stlr instructions providing sequentially consistent atomic load and store. These were targeted to C++, which does not define the behavior of any program with a data race. Unsurprisingly, then, the behavior of these instructions in racy programs did not match the expectations of the ES2017 authors, and in particular it did not satisfy the ES2017 requirements for racy program behavior.

Litmus Test: ES2017 racy reads on ARMv8
Can this program (using atomics) see r1 = 0, r2 = 1?

// Thread 1           // Thread 2
x = 1                 y = 1
r1 = y                x = 2 (non-atomic)
                      r2 = x

C++: yes (data race, can do anything at all).
Java: the program cannot be written.
ARMv8 using ldar/stlr: yes.
ES2017: no! (contradicting ARMv8)

In this program, all the reads and writes are sequentially consistent atomics with the exception of x = 2: thread 1 writes x = 1 using an atomic store, but thread 2 writes x = 2 using a non-atomic store. In C++, this is a data race, so all bets are off. In Java, this program cannot be written: x must either be declared volatile or not; it can’t be accessed atomically only sometimes. In ES2017, the memory model turns out to disallow r1 = 0, r2 = 1. If r1 = y reads 0, thread 1 must complete before thread 2 begins, in which case the non-atomic x = 2 would seem to happen after and overwrite the x = 1, causing the atomic r2 = x to read 2. This explanation seems entirely reasonable, but it is not the way ARMv8 processors work.

It turns out that, for the equivalent sequence of ARMv8 instructions, the non-atomic write to x can be reordered ahead of the atomic write to y, so that this program does in fact produce r1 = 0, r2 = 1. This is not a problem in C++, since the race means the program can do anything at all, but it is a problem for ES2017, which limits racy behaviors to a set of outcomes that does not include r1 = 0, r2 = 1.

Since it was an explicit goal of ES2017 to use the ARMv8 instructions to implement the sequentially consistent atomic operations, Watt et al. reported that their suggested fixes, slated to be included in the next revision of the standard, would weaken the racy behavior constraints just enough to allow this outcome. (It is unclear to me whether at the time “next revision” meant ES2020 or ES2021.)

Watt et al.’s suggested changes also included a fix to a second bug, first identified by Watt, Andreas Rossberg, and Jean Pichon-Pharabod, wherein a data-race-free program was not given sequentially consistent semantics by the ES2017 specification. That program is given by:

Litmus Test: ES2017 data-race-free program
Can this program (using atomics) see r1 = 1, r2 = 2?

// Thread 1           // Thread 2
x = 1                 x = 2
                      r1 = x
                      if (r1 == 1) {
                          r2 = x // non-atomic
                      }

On sequentially consistent hardware: no.
C++: I’m not enough of a C++ expert to say for sure.
Java: the program cannot be written.
ES2017: yes! (violating DRF-SC).

In this program, all the reads and writes are sequentially consistent atomics with the exception of r2 = x, as marked. This program is data-race-free: the non-atomic read, which would have to be involved in any data race, only executes when r1 = 1, which proves that thread 1’s x = 1 happens before the r1 = x and therefore also before the r2 = x. DRF-SC means that the program must execute in a sequentially consistent manner, so that r1 = 1, r2 = 2 is impossible, but the ES2017 specification allowed it.

The ES2017 specification of program behavior was therefore simultaneously too strong (it disallowed real ARMv8 behavior for racy programs) and too weak (it allowed non-sequentially consistent behavior for race-free programs). As noted earlier, these mistakes are fixed. Even so, this is yet another reminder about how subtle it can be to specify the semantics of both data-race-free and racy programs exactly using happens-before, as well as how subtle it can be to match up language memory models with the underlying hardware memory models.

It is encouraging that at least for now JavaScript has avoided adding any other atomics besides the sequentially consistent ones and has resisted “DRF-SC or Catch Fire.” The result is a memory model valid as a C/C++ compilation target but much closer to Java.

Conclusions

Looking at C, C++, Java, JavaScript, Rust, and Swift, we can make the following observations:

Meanwhile, processor manufacturers seem to have accepted that the abstraction of sequentially consistent synchronizing atomics is important to implement efficiently and are starting to do so: ARMv8 and RISC-V both provide direct support.

Finally, a truly immense amount of verification and formal analysis work has gone into understanding these systems and stating their behaviors precisely. It is particularly encouraging that Watt et al. were able in 2020 to give a formal model of a significant subset of JavaScript and use a theorem prover to prove correctness of compilation to ARM, POWER, RISC-V, and x86-TSO.

Twenty-five years after the first Java memory model, and after many person-centuries of research effort, we may be starting to be able to formalize entire memory models. Perhaps, one day, we will also fully understand them.

The next post in this series is “Updating the Go Memory Model.”

Acknowledgements

This series of posts benefited greatly from discussions with and feedback from a long list of engineers I am lucky to work with at Google. My thanks to them. I take full responsibility for any mistakes or unpopular opinions.