Zip Files All The Way Down
Posted on Thursday, March 18, 2010.
Stephen Hawking begins A Brief History of Time with this story:
A well-known scientist (some say it was Bertrand Russell) once gave a public lecture on astronomy. He described how the earth orbits around the sun and how the sun, in turn, orbits around the center of a vast collection of stars called our galaxy. At the end of the lecture, a little old lady at the back of the room got up and said: “What you have told us is rubbish. The world is really a flat plate supported on the back of a giant tortoise.” The scientist gave a superior smile before replying, “What is the tortoise standing on?” “You're very clever, young man, very clever,” said the old lady. “But it's turtles all the way down!”
Scientists today are pretty sure that the universe is not actually turtles all the way down, but we can create that kind of situation in other contexts. For example, here we have video monitors all the way down and set theory books all the way down, and shopping carts all the way down.
And here's a computer storage equivalent:
look inside r.zip.
It's zip files all the way down:
each one contains another zip file under the name r/r.zip.
(For the die-hard Unix fans, r.tar.gz is
gzipped tar files all the way down.)
Like the line of shopping carts, it never ends,
because it loops back onto itself: the zip file contains itself!
And it's probably less work to put together a self-reproducing zip file
than to put together all those shopping carts,
at least if you're the kind of person who would read this blog.
This post explains how.
Before we get to self-reproducing zip files, though, we need to take a brief detour into self-reproducing programs.
Self-reproducing programs
The idea of self-reproducing programs dates back to the 1960s. My favorite statement of the problem is the one Ken Thompson gave in his 1983 Turing Award address:
In college, before video games, we would amuse ourselves by posing programming exercises. One of the favorites was to write the shortest self-reproducing program. Since this is an exercise divorced from reality, the usual vehicle was FORTRAN. Actually, FORTRAN was the language of choice for the same reason that three-legged races are popular.
More precisely stated, the problem is to write a source program that, when compiled and executed, will produce as output an exact copy of its source. If you have never done this, I urge you to try it on your own. The discovery of how to do it is a revelation that far surpasses any benefit obtained by being told how to do it. The part about “shortest” was just an incentive to demonstrate skill and determine a winner.
Spoiler alert! I agree: if you have never done this, I urge you to try it on your own. The internet makes it so easy to look things up that it's refreshing to discover something yourself once in a while. Go ahead and spend a few days figuring out. This blog will still be here when you get back. (If you don't mind the spoilers, the entire Turing award address is worth reading.)
(Spoiler blocker.)

http://www.robertwechsler.com/projects.html
Let's try to write a Python program that prints itself.
It will probably be a print statement, so here's a first attempt,
run at the interpreter prompt:
>>> print 'hello'
hello
That didn't quite work. But now we know what the program is, so let's print it:
>>> print "print 'hello'"
print 'hello'
That didn't quite work either. The problem is that when you execute a simple print statement, it only prints part of itself: the argument to the print. We need a way to print the rest of the program too.
The trick is to use recursion: you write a string that is the whole program, but with itself missing, and then you plug it into itself before passing it to print.
>>> s = 'print %s'; print s % repr(s)
print 'print %s'
Not quite, but closer: the problem is that the string s isn't actually
the program. But now we know the general form of the program:
s = '%s'; print s % repr(s).
That's the string to use.
>>> s = 's = %s; print s %% repr(s)'; print s % repr(s)
s = 's = %s; print s %% repr(s)'; print s % repr(s)
Recursion for the win.
This form of self-reproducing program is often called a quine, in honor of the philosopher and logician W. V. O. Quine, who discovered the paradoxical sentence:
“Yields falsehood when preceded by its quotation”
yields falsehood when preceded by its quotation.
The simplest English form of a self-reproducing quine is a command like:
Print this, followed by its quotation:
“Print this, followed by its quotation:”
There's nothing particularly special about Python that makes quining possible. The most elegant quine I know is a Scheme program that is a direct, if somewhat inscrutable, translation of that sentiment:
((lambda (x) `(,x ',x)) '(lambda (x) `(,x ',x)))
I think the Go version is a clearer translation, at least as far as the quoting is concerned:
/* Go quine */ package main import "fmt" func main() { fmt.Printf("%s%c%s%c\n", q, 0x60, q, 0x60) } var q = `/* Go quine */ package main import "fmt" func main() { fmt.Printf("%s%c%s%c\n", q, 0x60, q, 0x60) } var q = `
(I've colored the data literals green throughout to make it clear what is program and what is data.)
The Go program has the interesting property that, ignoring the pesky newline
at the end, the entire program is the same thing twice (/* Go quine */ ... q = `).
That got me thinking: maybe it's possible to write a self-reproducing program
using only a repetition operator.
And you know what programming language has essentially only a repetition operator?
The language used to encode Lempel-Ziv compressed files
like the ones used by gzip and zip.
Self-reproducing Lempel-Ziv programs
Lempel-Ziv compressed data is a stream of instructions with two basic
opcodes: literal(n) followed by
n bytes of data means write those n bytes into the
decompressed output,
and repeat(d, n)
means look backward d bytes from the current location
in the decompressed output and copy the n bytes you find there
into the output stream.
The programming exercise, then, is this: write a Lempel-Ziv program
using just those two opcodes that prints itself when run.
In other words, write a compressed data stream that decompresses to itself.
Feel free to assume any reasonable encoding for the literal
and repeat opcodes.
For the grand prize, find a program that decompresses to
itself surrounded by an arbitrary prefix and suffix,
so that the sequence could be embedded in an actual gzip
or zip file, which has a fixed-format header and trailer.
Spoiler alert! I urge you to try this on your own before continuing to read. It's a great way to spend a lazy afternoon, and you have one critical advantage that I didn't: you know there is a solution.
(Spoiler blocker.)
.jpg)
http://www.robertwechsler.com/thebest.html
By the way, here's r.gz, gzip files all the way down.
$ gunzip < r.gz > r $ cmp r r.gz $
The nice thing about r.gz is that even broken web browsers
that ordinarily decompress downloaded gzip data before storing it to disk
will handle this file correctly!
Enough stalling to hide the spoilers.
Let's use this shorthand to describe Lempel-Ziv instructions:
Ln and Rn are
shorthand for literal(n) and
repeat(n, n),
and the program assumes that each code is one byte.
L0 is therefore the Lempel-Ziv no-op;
L5 hello prints hello;
and so does L3 hel R1 L1 o.
Here's a Lempel-Ziv program that prints itself. (Each line is one instruction.)
| Code | Output | |||
|---|---|---|---|---|
| no-op | L0 | |||
| no-op | L0 | |||
| no-op | L0 | |||
| print 4 bytes | L4 L0 L0 L0 L4 | L0 L0 L0 L4 | ||
| repeat last 4 printed bytes | R4 | L0 L0 L0 L4 | ||
| print 4 bytes | L4 R4 L4 R4 L4 | R4 L4 R4 L4 | ||
| repeat last 4 printed bytes | R4 | R4 L4 R4 L4 | ||
| print 4 bytes | L4 L0 L0 L0 L0 | L0 L0 L0 L0 |
(The two columns Code and Output contain the same byte sequence.)
The interesting core of this program is the 6-byte sequence
L4 R4 L4 R4 L4 R4, which prints the 8-byte sequence R4 L4 R4 L4 R4 L4 R4 L4.
That is, it prints itself with an extra byte before and after.
When we were trying to write the self-reproducing Python program,
the basic problem was that the print statement was always longer
than what it printed. We solved that problem with recursion,
computing the string to print by plugging it into itself.
Here we took a different approach.
The Lempel-Ziv program is
particularly repetitive, so that a repeated substring ends up
containing the entire fragment. The recursion is in the
representation of the program rather than its execution.
Either way, that fragment is the crucial point.
Before the final R4, the output lags behind the input.
Once it executes, the output is one code ahead.
The L0 no-ops are plugged into
a more general variant of the program, which can reproduce itself
with the addition of an arbitrary three-byte prefix and suffix:
| Code | Output | |||
|---|---|---|---|---|
| print 4 bytes | L4 aa bb cc L4 | aa bb cc L4 | ||
| repeat last 4 printed bytes | R4 | aa bb cc L4 | ||
| print 4 bytes | L4 R4 L4 R4 L4 | R4 L4 R4 L4 | ||
| repeat last 4 printed bytes | R4 | R4 L4 R4 L4 | ||
| print 4 bytes | L4 R4 xx yy zz | R4 xx yy zz | ||
| repeat last 4 printed bytes | R4 | R4 xx yy zz |
(The byte sequence in the Output column is aa bb cc, then
the byte sequence from the Code column, then xx yy zz.)
It took me the better part of a quiet Sunday to get this far,
but by the time I got here I knew the game was over
and that I'd won.
From all that experimenting, I knew it was easy to create
a program fragment that printed itself minus a few instructions
or even one that printed an arbitrary prefix
and then itself, minus a few instructions.
The extra aa bb cc in the output
provides a place to attach such a program fragment.
Similarly, it's easy to create a fragment to attach
to the xx yy zz that prints itself,
minus the first three instructions, plus an arbitrary suffix.
We can use that generality to attach an appropriate
header and trailer.
Here is the final program, which prints itself surrounded by an
arbitrary prefix and suffix.
[P] denotes the p-byte compressed form of the prefix P;
similarly, [S] denotes the s-byte compressed form of the suffix S.
| Code | Output | |||
|---|---|---|---|---|
| print prefix | [P] |
P |
||
| print p+1 bytes | Lp+1 [P] Lp+1 |
[P] Lp+1 |
||
| repeat last p+1 printed bytes | Rp+1 |
[P] Lp+1 |
||
| print 1 byte | L1 Rp+1 |
Rp+1 |
||
| print 1 byte | L1 L1 |
L1 |
||
| print 4 bytes | L4 Rp+1 L1 L1 L4 |
Rp+1 L1 L1 L4 |
||
| repeat last 4 printed bytes | R4 |
Rp+1 L1 L1 L4 |
||
| print 4 bytes | L4 R4 L4 R4 L4 |
R4 L4 R4 L4 |
||
| repeat last 4 printed bytes | R4 |
R4 L4 R4 L4 |
||
| print 4 bytes | L4 R4 L0 L0 Ls+1 |
R4 L0 L0 Ls+1 |
||
| repeat last 4 printed bytes | R4 |
R4 L0 L0 Ls+1 |
||
| no-op | L0 |
|||
| no-op | L0 |
|||
| print s+1 bytes | Ls+1 Rs+1 [S] |
Rs+1 [S] |
||
| repeat last s+1 bytes | Rs+1 |
Rs+1 [S] |
||
| print suffix | [S] |
S |
(The byte sequence in the Output column is P, then
the byte sequence from the Code column, then S.)
Self-reproducing zip files
Now the rubber meets the road. We've solved the main theoretical obstacle to making a self-reproducing zip file, but there are a couple practical obstacles still in our way.
The first obstacle is to translate our self-reproducing Lempel-Ziv program, written in simplified opcodes, into the real opcode encoding. RFC 1951 describes the DEFLATE format used in both gzip and zip: a sequence of blocks, each of which is a sequence of opcodes encoded using Huffman codes. Huffman codes assign different length bit strings to different opcodes, breaking our assumption above that opcodes have fixed length. But wait! We can, with some care, find a set of fixed-size encodings that says what we need to be able to express.
In DEFLATE, there are literal blocks and opcode blocks. The header at the beginning of a literal block is 5 bytes:

If the translation of our L opcodes above
are 5 bytes each, the translation of the R opcodes
must also be 5 bytes each, with all the byte counts
above scaled by a factor of 5.
(For example, L4 now has a 20-byte argument,
and R4 repeats the last 20 bytes of output.)
The opcode block
with a single repeat(20,20) instruction falls well short of
5 bytes:

Luckily, an opcode block containing two
repeat(20,10) instructions has the same effect and is exactly 5 bytes:
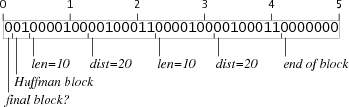
Encoding the other sized repeats
(Rp+1 and
Rs+1)
takes more effort
and some sleazy tricks, but it turns out that
we can design 5-byte codes that repeat any amount
from 9 to 64 bytes.
For example, here are the repeat blocks for 10 bytes and for 40 bytes:
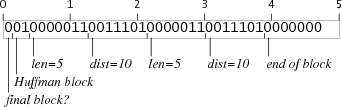
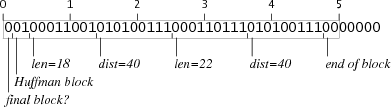
The repeat block for 10 bytes is two bits too short, but every repeat block is followed by a literal block, which starts with three zero bits and then padding to the next byte boundary. If a repeat block ends two bits short of a byte but is followed by a literal block, the literal block's padding will insert the extra two bits. Similarly, the repeat block for 40 bytes is five bits too long, but they're all zero bits. Starting a literal block five bits too late steals the bits from the padding. Both of these tricks only work because the last 7 bits of any repeat block are zero and the bits in the first byte of any literal block are also zero, so the boundary isn't directly visible. If the literal block started with a one bit, this sleazy trick wouldn't work.
The second obstacle is that zip archives (and gzip files) record a CRC32 checksum of the uncompressed data. Since the uncompressed data is the zip archive, the data being checksummed includes the checksum itself. So we need to find a value x such that writing x into the checksum field causes the file to checksum to x. Recursion strikes back.
The CRC32 checksum computation interprets the entire file as a big number and computes the remainder when you divide that number by a specific constant using a specific kind of division. We could go through the effort of setting up the appropriate equations and solving for x. But frankly, we've already solved one nasty recursive puzzle today, and enough is enough. There are only four billion possibilities for x: we can write a program to try each in turn, until it finds one that works.
If you want to recreate these files yourself, there are a
few more minor obstacles, like making sure the tar file is a multiple
of 512 bytes and compressing the rather large zip trailer to
at most 59 bytes so that Rs+1 is
at most R64.
But they're just a simple matter of programming.
So there you have it:
r.gz (gzip files all the way down),
r.tar.gz (gzipped tar files all the way down),
and
r.zip (zip files all the way down).
I regret that I have been unable to find any programs
that insist on decompressing these files recursively, ad infinitum.
It would have been fun to watch them squirm, but
it looks like much less sophisticated
zip bombs have spoiled the fun.
If you're feeling particularly ambitious, here is rgzip.go, the Go program that generated these files. I wonder if you can create a zip file that contains a gzipped tar file that contains the original zip file. Ken Thompson suggested trying to make a zip file that contains a slightly larger copy of itself, recursively, so that as you dive down the chain of zip files each one gets a little bigger. (If you do manage either of these, please leave a comment.)
P.S. I can't end the post without sharing my favorite self-reproducing program: the one-line shell script #!/bin/cat.
(Comments originally posted via Blogger.)
Marius Gedminas (March 18, 2010 9:22 AM) It's been done before, but I liked your writeup better.
tafs (March 18, 2010 9:46 AM) In Safari on Mac OS X, with the option 'open "safe" files after downloading' set (on by default), it keeps uncompressing and filling up my disk. "safe" indeed …
Aaron Davies (March 18, 2010 1:59 PM) > #!/bin/cat
very nice. i'm kind of partial to "10 LIST", myself....
Shahms (March 18, 2010 3:46 PM) It's kind of cheating, but in Python you can write arbitrary self-repeating programs pretty trivially (if you assume the standard library as well):
import inspect, sys
print inspect.getsource(sys.modules['__main__']),
EthanG (March 18, 2010 4:39 PM) @tafs: at least it responds to the cancel button in the downloads window. Mine got to r-962 (963 unpacks) before I killed it, for a total of 3.8MB in the trash.
Nick (March 18, 2010 6:23 PM) This post has been removed by the author.
Nick (March 18, 2010 6:25 PM) Perhaps r.zip could contain two copies of itself ...
Reminds me of "I cannot be played on a record player X" ...
luc (March 19, 2010 7:18 AM) C's handling of strings make it slightly annoying but not overly complicated... I'd like to know if anyone can come up with anything shorter (but still in bare C).
char qs[160]; char *q(char *s){char *rs=qs;do{if(*s==0x22)*(rs++)=0x5C;*(rs++)=*s;}while(*(s++));return qs;} int main() { char *s = "char qs[160]; char *q(char *s){char *rs=qs;do{if(*s==0x22)*(rs++)=0x5C;*(rs++)=*s;}while(*(s++));return qs;} int main() { char *s = \"%s\"; printf(s, q(s)); }"; printf(s, q(s)); }
luc (March 19, 2010 7:21 AM) Despite slight annoiances related to string handling, a C version is relatively short (closest fragment to an IOCCC candidate I have ever written ;) ) :
char qs[160]; char *q(char *s){char *rs=qs;do{if(*s==0x22)*(rs++)=0x5C;*(rs++)=*s;}while(*(s++));return qs;} int main() { char *s = "char qs[160]; char *q(char *s){char *rs=qs;do{if(*s==0x22)*(rs++)=0x5C;*(rs++)=*s;}while(*(s++));return qs;} int main() { char *s = \"%s\"; printf(s, q(s)); }"; printf(s, q(s)); }
luc (March 19, 2010 7:22 AM) Sorry about the double posting, my browser returned a 404 on the first attempt...
Arachnid (March 19, 2010 9:19 AM) Any hints on how you would write a version that unpacks to a larger copy of itself, given the crc32 issue?
Russ Cox (March 19, 2010 10:08 AM) @Arachnid: I suspect you could engineer a sequence that when inserted into a specific place (no matter how many times) would leave the crc unaffected. But I haven't done the math.
nickjohnson (March 19, 2010 10:13 AM) That occurred to me shortly afterwards. In principle it shouldn't be hard, since CRCs only correct for small errors. If the sequence is a set of instructions that print itself twice, you're sorted!
ajshankar (March 22, 2010 12:40 PM) Fascinating post!
Is it possible to create a pure LZ quine (without header or footer) that doesn't use L0 no-ops?
ajshankar (March 23, 2010 10:39 AM) For the record, the answer is yes, and it can be done with this 16-opcode quine (your easier-to-explain solution was 20):
L2 L2 L2
L2 L2 L2
L2 L2 L2
R4,3
L4 R4,3 L4 R4,3 L4
R4,3
And the shortest one I've found is 14 opcodes:
L0
L4 L0 L4 L0 L4
L0
R4,3
L4 R4,3 L4 R4,3 L4
R4,3
Russ Cox (March 23, 2010 12:05 PM) Neat. If you start with the core pattern from above you can plug in L1 L1 L1 L1 L1 L1 on both ends instead of L0 L0 L0, but that's even longer.
The link in the first comment boils down to this 9-instruction one. It takes advantage of the fact that you can have a repeat length longer than the back-up
L0
L2 L0 L2
L0
R2,3
L2 R2,3 L2
R2,3
(R2,3 == go back 2 bytes and copy 3: if the current output ends with x y, that appends x y x.)
ajshankar (March 23, 2010 12:20 PM) Dang, that's sneaky. I like it. I happened on the 4,3 approach after I got frustrated with trying to find a pure 3,2 solution. But I never thought to do 2,3.
Misi (March 24, 2010 2:56 PM) About CRC: you can modify your program to contain an arbitrary 4 byte sequence somewhere (exactly once). And by modifying these 4 bytes you can make the CRC to be anything.
So, you first chose your CRC (for example to be 0x00000000), create your self-reproducing archive, and finally chose that 4 bytes so that CRC is what you want it to be. Thus, avoiding the recursive problem altogether.
k5 user (March 25, 2010 11:54 AM) Late for the game, but recursive zips have been around a very very long time. The anti-virus world has known about them for at least 8 years. One could create a denial of service attack against an AV product that was set to scan compressed files by sending in a zip of death. To combat this, many AV programs stop processing after some configurable "depth" into the file.
Misi (March 27, 2010 9:12 AM) So, here's what I was talking about:
rec_fix.gz
It is a gzip quine, in which the bytes 102-105 are "fix points". That is, you can change them to whatever you want and the file will still uncompress to itself. (Of course, if you change them the CRC won't check out.)
So, I created this file with CRC in gzip footer set to all 0, and then "reverse computed" the CRC in these four bytes, so that the CRC of the whole file is actually 0. I believe, that based on this idea it is possible to create a file that has a part in the middle, which duplicate itself on gunzipping, while the CRC stays the same. I will post it here when I'm finished.
You also might want to look inside this file, as it is based on slightly different idea than yours. For example, I do not depend on "repeat" opcodes being 5 bytes. There's a "source code" which might be slightly easier to read: rec_fix.lgz
Misi (March 27, 2010 3:47 PM) Here it is: rec_exp.gz.
It has a 32 bytes block which duplicates on uncompressing, and the CRC is always correct (and 0).
Unfortunately, the gzip footer also contains a size field, which of course won't be correct... Until you uncompress the file 27 times. :) At that point the size of the duplicating block will become 4 gigabytes and the 32 bit size field is set to be the remainder. (I didn't check this though. :))
While thinking about this, I realized that there is a much simpler (but somewhat cheating) way of creating a "growing gzip quine". You just duplicate the whole file. As gzip just concatenates the output of concatenated inputs, this will work without paying much attention to size or crc fields. So, here is a file for which gunzipping is the same as concatenating it with itself: rec_dup.gz
(The "sources" are available in the same directory.)
Marc Ruef (May 1, 2010 1:57 AM) Hello,
Very interesting research and a great writeup! Keep up the good work.
Regards,
Marc
user-unknown (May 1, 2010 3:23 PM) Here is my rather unknown quine:
import java.math.BigInteger;
/**
(c) Stefan Wagner, GPLv3.0
*/
class Quine
{
public static void main (String [] args)
{
BigInteger b = new BigInteger ("3125672623196693767569686149189009633452 2377871159551965921417137170609691214223 9208376749605139774443708326203800130556 5247549291738666720120851102563432688661 2425053632619026133552590824825360959495 9103568388341399920152904163137391991148 8600579488934249116624219425362354637760 9935667840623358056717110027295132562103 9400252768836739128617742678124740473856 7878670179316536315099060433926849016933 4865116792986969613917692005305319947405 7778267800604078704652663104779321903695 4971735707525104532138973326414147694788 6144049586837524382107377428450195285880 0467794888319592557310425481240448120408 1531669064199685228190893676717975716990 4846241527401973665847012561439332697517 5470668411522967977332908759408086343490 26570");
int i=0;
for (byte c : b.toByteArray ())
{
++i;
if (i==159)
System.out.print (b);
System.out.print ((char)c);
}
}
}
And here my shortest bash-quine:. Yes, that it was. Maybe you didn't see it - here is how you produce it:
touch _; chmod a+x _; ./_
steffenz (May 2, 2010 10:02 AM) In Perl (one line without newline):
$q=chr(39);$s='$q=chr(39);$s=%s%s%s; printf $s,$q,$s,$q;'; printf $s,$q,$s,$q;
steffenz (May 3, 2010 3:18 AM) And the C version is just the same (one line without newline):
main(){char q=34; char *s="main(){char q=34; char *s=%c%s%c; printf(s,q,s,q);}"; printf(s,q,s,q);}
DAGwyn (May 19, 2010 4:31 AM) Hioefukky any antivirus program that stops after some fixed depth then flags the file as malware, rather than treating it as benign. The main reason is that the hackers will obviously just hide their malware in a nested ZIP file one level deeper than the threshold.
Duncan (May 25, 2010 5:52 AM) "I regret that I have been unable to find any programs that insist on decompressing these files recursively, ad infinitum. It would have been fun to watch them squirm, but it looks like much less sophisticated zip bombs have spoiled the fun."
I'm afraid I have found something that bombs. I thought this was fun so I last week emailed a copy of r.zip to a few colleagues at work. Today the mail servers crashed.
Our email is Lotus Notes with McAfee as a virus scanner. It seems that while the desktop version of McAfee only scans a zip file when you unzip it, the server version checks every emailed zip file right the way down...
It seems to have taken it a week to fill the disc.
Franz (November 4, 2010 5:25 AM) Computer scientists all the way down
Beautiful post, thank you!
But I find very misleading the shopping cart metaphor. The key
to a quine is to have something (the program) that contains a
representation of itself (the string to be printed). Finally, the act
of representing the representation (executing the 'print' instruction)
makes the representation real (a new program, identical to its
parent). There's no representation of a cart in circle of carts.
Other artistic context have the potentiality of making quines, as they
blur the boundary between reality and its representation. I'm thinking
about some of Escher's drawings, Pirandello's "six characters in
search of an author", or Allen's "Purple Rose of Cairo".
However none of them is a quine, because the artistic work does not
represent itself (e.g."Purple Rose of Cairo"'s representation is a
movie about egypt, rather than a Great Depression story).
The example that gets closer to a real quine (probably by accident) is
"The 13th floor". (spoiler ahead)
In the movie a team of computer scientists in Los Angeles creates a
simulation of Los Angeles, only to discover that they are themselves
part of a computer simulation made by a team of Los Angeles
scientists. The silly authors stop the movie at three levels (in the
innermost Los Angeles the year is 1937, and there are no
computers). But just wait enough (cpu) time... and it's going to be
computer scientists all the way down!
Aaron Davies (November 4, 2010 5:36 AM) also eXistenZ, and of course now Inception. in books, there's house of leaves and various things by borjes and nabakov.
AndyMm (November 29, 2010 2:00 PM) In Javascript using Integers.
c=[59,21,51,,53,19,62,71,74,0,57,21,58,21,51,53,19,57,20,14,13,19,57,3,3,1,58,3,21,57,54,11,23,
43,76,74,65,70,63,6,62,74,71,69,27,64,57,74,27,71,60,61,0,59,51,3,57,53,3,12,8,1,18,59,19];
for(a=b=[];a<65;a++)b+=a^3?String.fromCharCode(c[+a]+40):c;
using RegExp. Seen people use RegExp in more crazier ways, but here is a simple one.
unescape(q=/unescape%28q=%2FQ%2F%5B-1%5D%29.replace%28%2FQ%2F,q%29/[-1]).replace(/Q/,q)
rhialto (January 7, 2011 1:50 PM) "The 13th floor" is a film version of a book by Daniel Galouye, "Simulacron 3". http://en.wikipedia.org/wiki/Simulacron-3
Also made into a film by Fassbinder.
Michael Mol (March 8, 2011 8:44 AM) Over at Rosetta Code, we have a page on Quines.
cacoyi (March 15, 2011 2:47 AM) I'm trying to compile your code so I can modify it to get similar results to this http://www.steike.com/code/useless/zip-file-quine/, but I'm getting these errors:
rgzip.go:347: undefined: bytes.Add
rgzip.go:700: too many arguments to panic: panic("cannot encode REP", n)
rgzip.go:710: undefined: flate.NewDeflater
rgzip.go:1057: cannot use &f.codebits (type *[19]int) as type []int in function argument
being new to go, can you point me in the right direction?
Anonymous (April 7, 2011 6:49 AM) @cacoyi:
bytes.Add was deleted from language. Changed to append
panic interprets literal as two arguments. Eleminated ",n"
flate.NewDeflater no longer exists. Changed to flate.NewWriter
codebits[numCodes]int drives program crazy. changed to codebits []int
Compiles now. Don't know if it works.
Anonymous (April 7, 2011 6:59 AM) @cacoyi:
bytes.Add was deleted from language. Changed to append
panic interprets literal as two arguments. Eleminated ",n"
flate.NewDeflater no longer exists. Changed to flate.NewWriter
codebits[numCodes]int drives program crazy. changed to codebits []int
Compiles now. Don't know if it works.
Anonymous (June 10, 2011 7:39 PM) I took your advice and tried to create one myself. I tried it with php, and it turned out to be trivial.
Simply put:
Will do it.
But I guess you are trying to make a different point.
Anonymous (June 10, 2011 7:40 PM) I took your advice and tried to create one myself. I tried it with php, and it turned out to be trivial.
Simply put:
<? php
print (file_get_contents(__FILE__));
?>
Will do it.
But I guess you are trying to make a different point.
Kela (July 17, 2011 9:48 AM) Unix Shell:
z=\' a='z=\\$z a=$z$a$z\; eval echo \$a'; eval echo $a
Cody (November 21, 2011 5:52 AM) I wrote about this the other day. As for the C versions, some of them have the problem of non compliance of the C standard (say, no int for main's return type). Another example is the implicit declaration of printf (no #include <stdio.h>)
So I fixed that stuff too (hopefully it pastes ok):
#include <stdio.h>
int main(){ char*p="#include <stdio.h>%cint main(){ char*p=%c%s%c; printf(p,10,34,p,34,10,10); return 0; %c}%c"; printf(p,10,34,p,34,10,10); return 0;
}
wc ran on that source file, for what its worth :
3 16 173 quine2.c
(For windows folks, that means : 3 lines, 16 words, 173 characters)
As for the person who tried it in php and included the file directly, indeed the point is very different. That's cheating and isn't a quine. If you include the file by reading it in in the source, that's hardly (as you point out) a challenge.
As for the author of this post, thanks for this - was interesting and fun. (I found it by way of looking up the zip file format for some reason I can't remember now; was I think referred to from wiki.)
Cody (November 21, 2011 6:04 AM) One other thing I forgot to reply to.
About antiviruses and recursive zip files: it's generally, at least from what I've seen, a user defined variable. Its not hard coded. So its not really flawed. The fact is that there's some things that will be hard to find out if it's ok or not on first look (and some av's may report it ok when others not, and so on). Even antidebugging tricks can make an antivirus detection engine think its malware when its not. Of course, the more 'scary' trick was piggybacking - that's when the malware would infect files/whatever as the av engine was scanning them.
Still, false positives are just as bad as a false negatives (another similar thing - badly configured firewalls can be really bad) when it comes to security. That's just how it goes, and we all have to make the best of it some times. Of course, if a file is zipped up many times it may bring about suspicion, and perhaps it should. What do they have to hide? So in the end it is a matter of using some common sense, understanding how things work, and antiviruses along with it does a pretty good job if all work together.
David Wagner (January 28, 2012 10:10 PM) This is awesome! Thank you for posting this puzzle.
I had fun looking at the simplified version, where you are only allowed Ln and Rn opcodes (Rn,m not allowed). I was curious what was the shortest quine.
For fun, I decided to throw a SAT solver at it. Here's what I found. The shortest quine is 16 bytes long:
L0 L0 L0 L2 L0 L0 L2 L0 L2 R3 R2 L2 R3 R2 R3 R2
Or, in parsed form:
L0
L0
L0
L2 L0 L0
L2 L0 L2
R3
R2
L2 R3 R2
R3
R2
Assuming my SAT code is correct, there is no shorter quine. There is also no quine of length 17. However, there appear to be quines of all larger lengths.
If you're curious how I encoded this as SAT, here's the approach I took to search for a quine of length n:
I defined a n-byte array of unknowns, call it In, so In(i) is the ith byte of the input. (We'll add constraints to force it to also be the ith byte of the output.)
Then, I defined a (n+1) x (n+1) array of boolean unknowns, active(.,.), where
active(i,j) is true if In(0..i-1) is a well-parsed sequence of bytes (i.e., it doesn't end in the middle of an unfinished string literal) and decompressing In(0..i-1) produces the output In(0..j-1).
It is not too difficult to write down a set of constraints that define the entries of active(.,.) in terms of the entries of In(.). I then emit constraints to require active(0,0) be true, and to require that active(n, n) be true. I then invoke the SAT solver to find a solution that respects all of these constraints.
This was fun! Thank you for sharing this puzzle.